Jumping Jack
*Tom Petty voice* FREE! FALLIN!
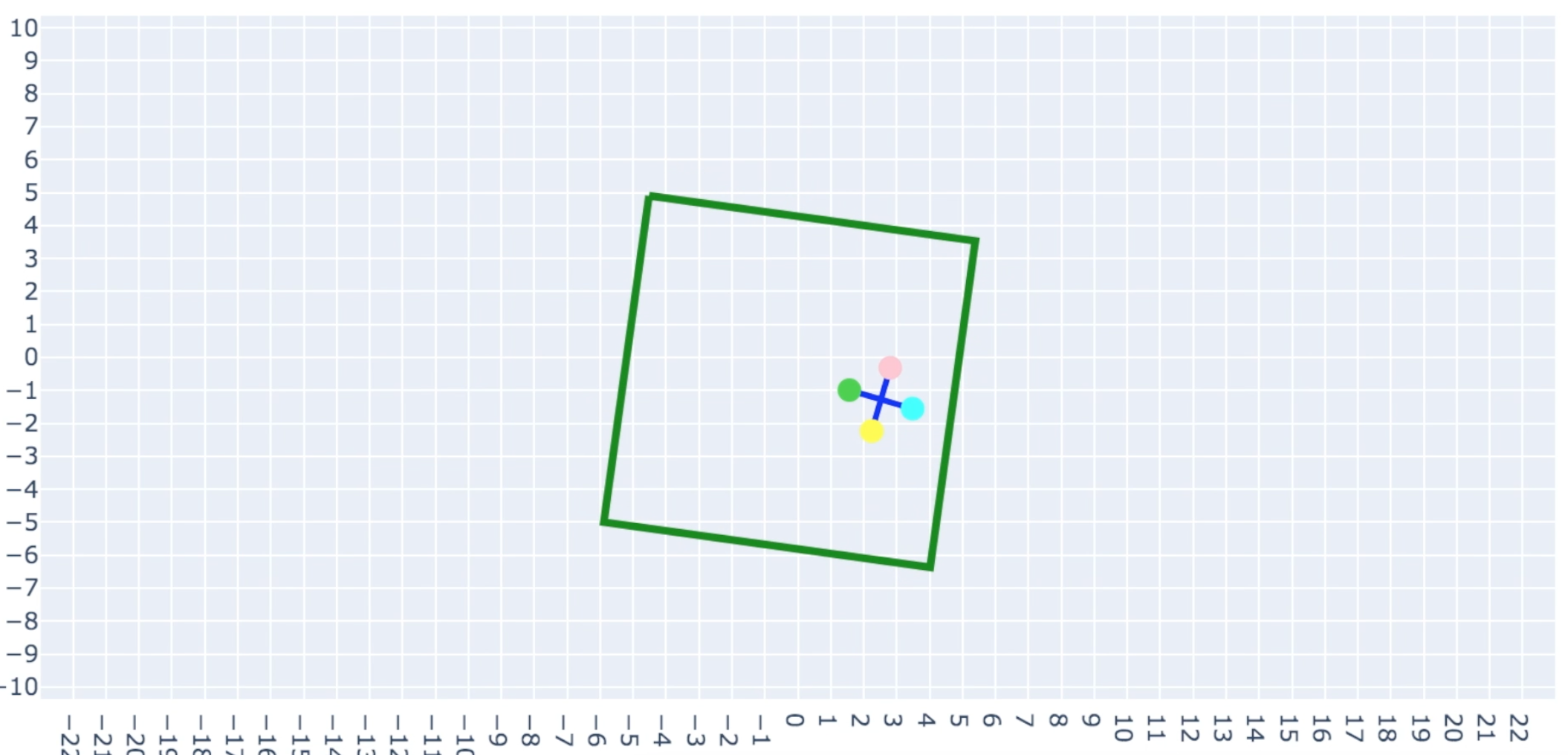
Overview:
The final project for Theory of Machine Dynamics that utilized Lagrangian dynamics to model and animate a chosen system.
The system involves two bodies (the jack and the box) and six degrees of freedom (x, y, and θ each for both the jack and the box). Both bodies experience rotational inertia, impacts, and external forces.
In order to keep the simulation feasible, the system is limited to 2D movement within a plane (as represented by the animation) and no spheres or circular shapes are involved to ensure that the impacts have some sort of nontrivial update.
The goal of this project is to calculate the trajectory of a jack in a box and animate the two objects' interaction with each other and their environment.
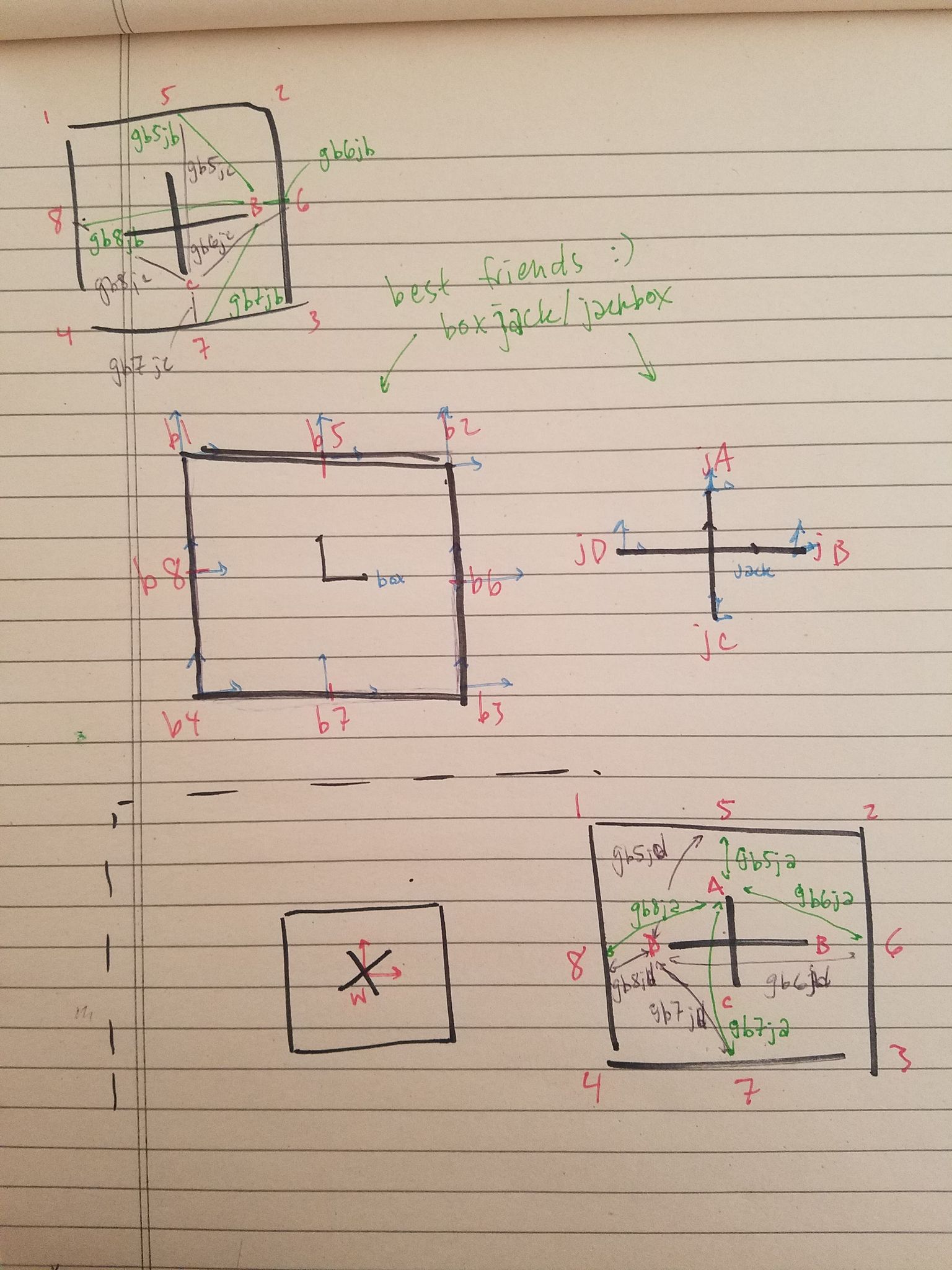
In the above diagram are all of the frames used with frame labels. It also includes all of the rigid body transformations used between the frames. These frames and their labels can also be found in the code.
Code:
The code is written exclusively in Python and requires the following packages:
* math: used to calculate quantities with pi
* matplotlib.pyplot: used to plot the trajectories of the box and jack over time
* numpy: used to perform matrix math calculations
* plotly.graph_objects: used in animation function for markers
* sympy:
used Function and symbols to define variables and dummy variables
used sin, cos, lambdify, Matrix, Eq, and solve for mathematical calculations
used simplify to expedite computations
* plotly.offline: used init_notebook_mode and iplot for animation function
* IPython.display: used display and HTML for animation function
* IPython.core.display: used HTML to display reference diagrams
Calculations:
Initialization:
Initialized the following parameters:
g = 9.8 (gravity) lb = 5 (length of box side) mb = 10 (mass of box) lj = 1 (length of jack) mj = 1 (mass of jack)
(functions, inc. derivatives)
xb = x_box yb = y_box thetab = theta_box xj = x_jack yj = y_jack thetaj = theta_jack q = all parameters
Euler-Lagrange equations:
Firstly, the Lagrangian was calculated with the equation:
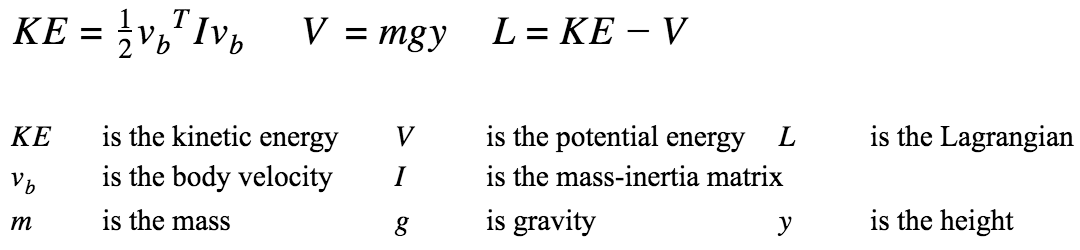
to get the following result:
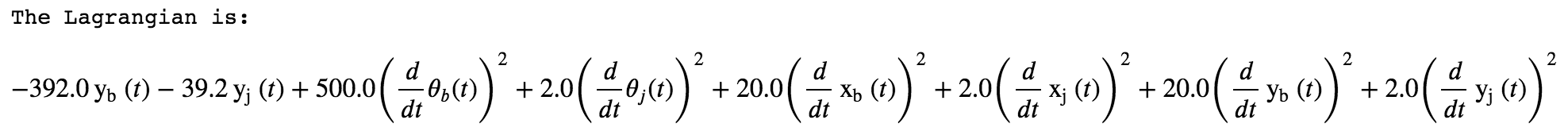
The calculate Lagrangian was then used in the eqation:
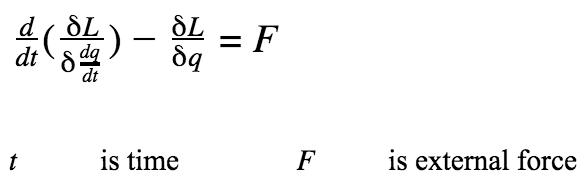
to get the Euler-Lagrange equations and solutions:

System constraints:
The constraints of this system are that the jack masses cannot leave the box, and will instead experience elastic impact with the walls (they will bounce). The external forces affect the y-coordinate of the box to keep it from falling straight off of the plot. To be completely honest, I wanted it to be [42 x gravity] for personal reasons, but that made the impacts too close together and freaked the system out. I settled for a close 41.
External forces:
The external force is written as: f = sym.Matrix([0, 41*g, 0, 0, 0, 0])
Impact update laws:
The impact updates for momentum and energy are calculated with the following equations:
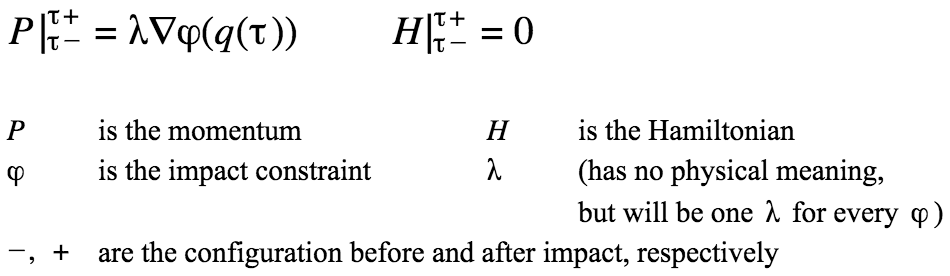
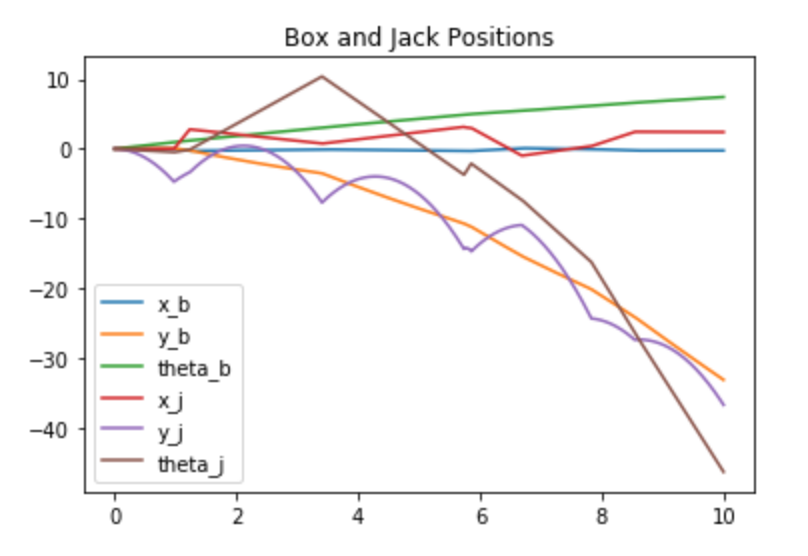
Results:
In the simulation, the box spins counter-clockwise and the jack simply falls (as defined in s0).
When the jack impacts the box, they both begin to fall since the jack exerts a force on the box.
The simulation ends with the jack and box barely remaining within the initial world frame.
This (hopefully) is correct since the jack is set to fall (but is much lighter than that of the box), but it still exerts enough force on the box to knock it downward.
As you can tell, I've taken a whole semester-long course in pedagogy and am a trained professional at explaining things (but only to people who think exactly the way I do).
Acknowledgements:
Huge thank you to the teaching staff, my bffs, Professor T. Murphey (there's an e in there!), soon-to-be Professor K. Fitzsimons, C. Porter, and MC. Sun :)
Special thanks also to all the people brave enough to ask questions during office hours and my coding friends who taught me to organize my thoughts.

